Normalverteilung

Die Normalverteilung ist eine der wichtigsten Verteilungen in der Statistik. Carl Friedrich Gauß (1777-1855) legte damit den Grundstein der modernen Statistik und entwickelte eine Verteilung, die auch heute noch zahlreiche Studierende um den Verstand bringt.

Du benötigst Unterstützung bei einer statistischen Auswertung oder eine Beratung? ProStat unterstützt dich professionell, schnell und freundlich. Du erreichst uns direkt per Telefon 0175 – 810 35 20 oder über das Kontaktformular.

Für dieses Wissensthema wird Grundlagenwissen zur z-Transformation benötigt und vorausgesetzt. Für alle Leser, die mit dieser statistischen Methode wenig oder gar keine Erfahrung haben, wird empfohlen, zunächst diesen Teil zu lesen. Mit der Normalverteilung besprechen wir ein sehr ausführliches Grundlagenwissen in der Statistik. Die Wahrscheinlichkeit der Normalverteilung (Fläche) werden wir mit der Tabelle der Normalverteilung (z-Werte) berechnen und analysieren und anhand von Beispielen erläutern, warum die Normalverteilung in der Statistik so wichtig ist.

Wahrscheinlichkeit

Den Begriff der Wahrscheinlichkeit benutzen wir praktisch unbewusst bereits mit der Anwendung der relativen Häufigkeit (Prozentwerte). Schauen wir uns dazu das Beispiel des IQs aus dem Thema der z-Transformation an (Abbildung 1).

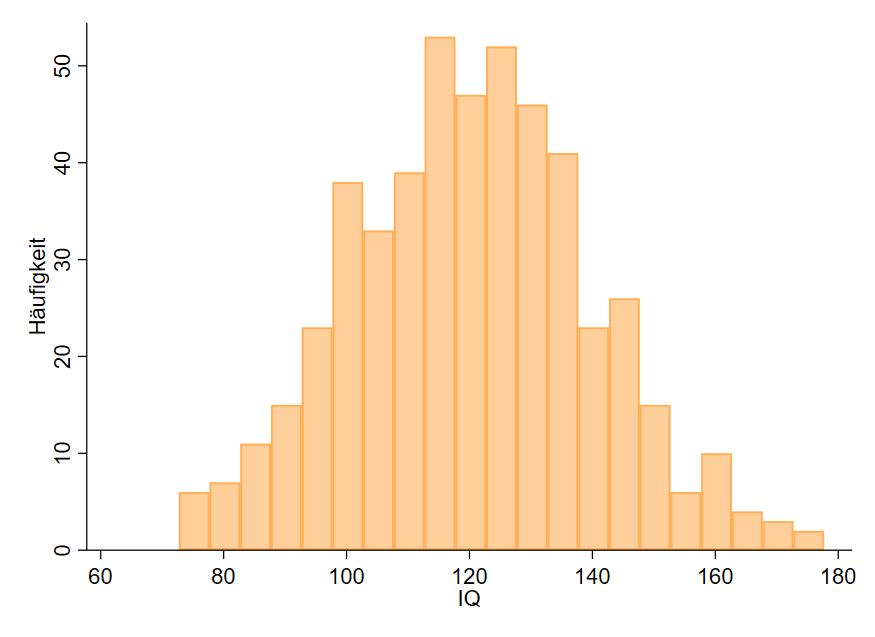
Deskriptive Kennwerte wie der Mittelwert interessieren uns an dieser Stelle zunächst nicht. Wir wissen von dieser Verteilung, dass $N=500$ Probanden am IQ-Test teilgenommen haben. Aus den Daten wissen wir außerdem, dass $N=15$ Probanden einen IQ $\geq$160 erreicht haben. Prozentual entspricht das $\frac{15}{500}=0.03=3\%$ der Probanden. Anders ausgedrückt können wir sagen, dass die Wahrscheinlichkeit, einen IQ von 160 oder größer zu haben $p=.03$ ist.

Die Wahrscheinlichkeit wird also in einem Wertebereich von 0 bis 1 ausgedrückt, was 0 bis 100 % entspricht, so ist $p=.23$ bspw. 23 %. Wir können die oben stehende Grafik anstatt mit der relativen Häufigkeit auch mit der Wahrscheinlichkeit $p$ darstellen (Abbildung 2).

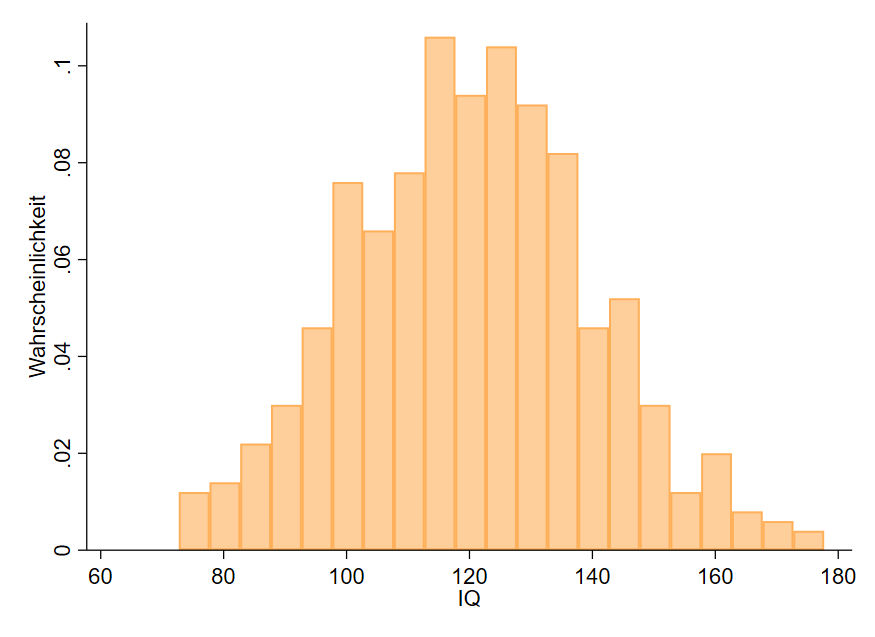
Die y-Achse enthält nun den Wert der Wahrscheinlichkeit $p$. Wenn wir wissen, dass der Balken bei einem IQ von 155 bis 165 bspw. $N=10$ Probanden enthält, dann ist die Wahrscheinlichkeit $p=\frac{10}{500}=.02$ also 2 %, dass ein Proband einen IQ von 155 bis 165 hat. Dies können wir an der y-Achse auch direkt ablesen. In Summe liegt die Wahrscheinlichkeit, irgendeinen IQ zu haben, bei $p=1$. Die Wahrscheinlichkeiten aller Balken ergeben insgesamt immer $p=1$.

“Normale” Normalverteilung

Der Titel klingt zunächst etwas seltsam, allerdings müssen wir an dieser Stelle den Unterschied zwischen einer Normalverteilung und der Standardnormalverteilung klären. Jede Verteilung hat nämlich eine dazu passende Normalverteilung. Abbildung 3 zeigt das uns bekannte Histogramm des IQs inklusive der Normalverteilungskurve für diese Daten.

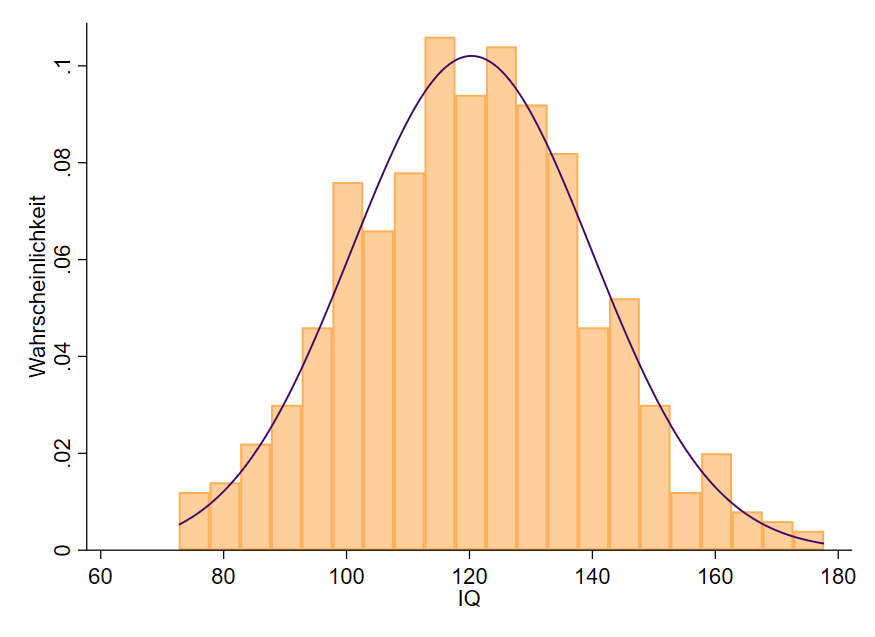
Wenn unsere IQ-Daten normalverteilt wären, müssten die Balken der Kurven folgen. Die Balken müssen dann immer unterhalb der Kurve liegen, ohne dass größere Lücken auftreten. Es sei an dieser Stelle angemerkt, dass der IQ in der Bevölkerung normalverteilt ist und unsere Daten daher recht gut in die Kurve passen. Weitere Informationen zum Thema Intelligenzquotient finden sich hier.

Es existieren also unendlich viele Normalverteilungskurven. Schauen wir uns z.B. eine Einkommensverteilung in einem Histogramm mit Normalverteilungskurve an (Abbildung 4).

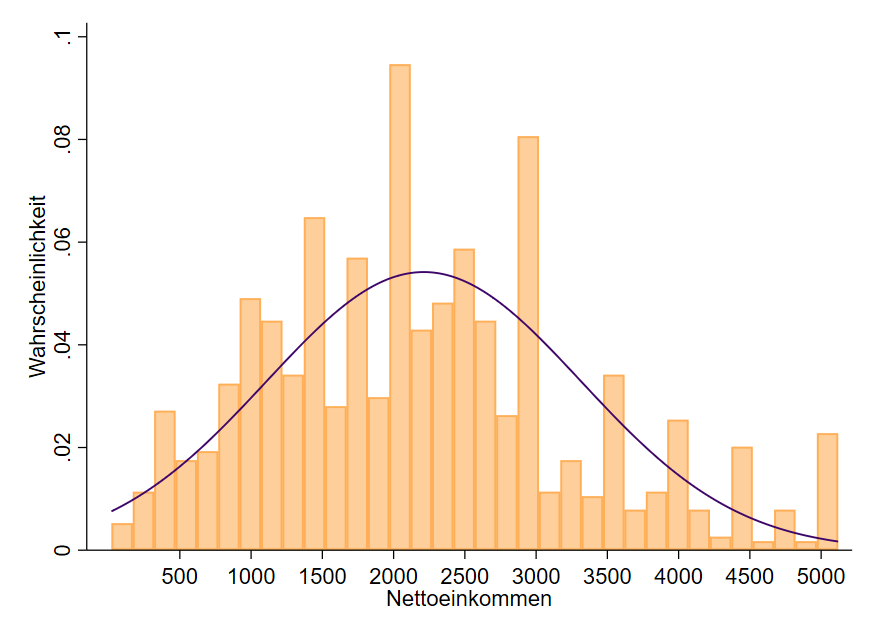
Wenn das Einkommen in diesen Daten normalverteilt wäre, dann müsste es der Kurve »folgen«. Wir sehen aber im Bereich von 2000 € einen Ausschlag über die Kurve sowie ab 3000 € größere Lücken unter der Kurve. Dies spricht optisch dafür, dass die Daten nicht normalverteilt sind. Zusammen mit einem Test auf Normalverteilung (Kolmogorow-Smirnow, Shapiro-Wilk) in einer Statistik-Software wär hier eine finale Einschätzung möglich.

Es existieren also unendlich viele Normalverteilungen. Die Normalverteilung des Einkommens in Abbildung 4 hat einen Mittelwert von ca. 2250 € und eine Standardabweichung von $s=287.716$ €. Die Normalverteilung des IQs hat einen Mittelwert von 120 und eine Standardabweichung von 11.459.

Statistisch gesehen ist ein Vergleich oder ein statistischer Test umständlich zu berechnen. Ideal wäre an dieser Stelle ein einheitlicher Vergleichsmaßstab. Daher gibt es die Standardnormalverteilung.

Standardnormalverteilung

Wer das Thema der z-Transformation gelesen hat oder sich damit auskennt weiß, dass eine z-Transformation den Mittelwert einer Variable auf Null ($\overline{x}=0$) festlegt und die Standardabweichung auf $s=1$. Damit haben wir praktisch schon den Weg zu einer der wichtigsten Verteilungen in der Statistik aufgezeigt, der Standardnormalverteilung. Das Wort Standard ist dabei von Bedeutung, da eine Standardnormalverteilung immer einen Mittelwert von $\overline{x}=0$ und eine Standardabweichung von $s=1$ aufweist. Aus diesem Grund können wir mit ihr auch statistisch sehr viel anfangen. Die unten stehende Grafik zeigt die Verteilung unseres z-transformierten IQs und die Standardnormalverteilung als lila Kurve.

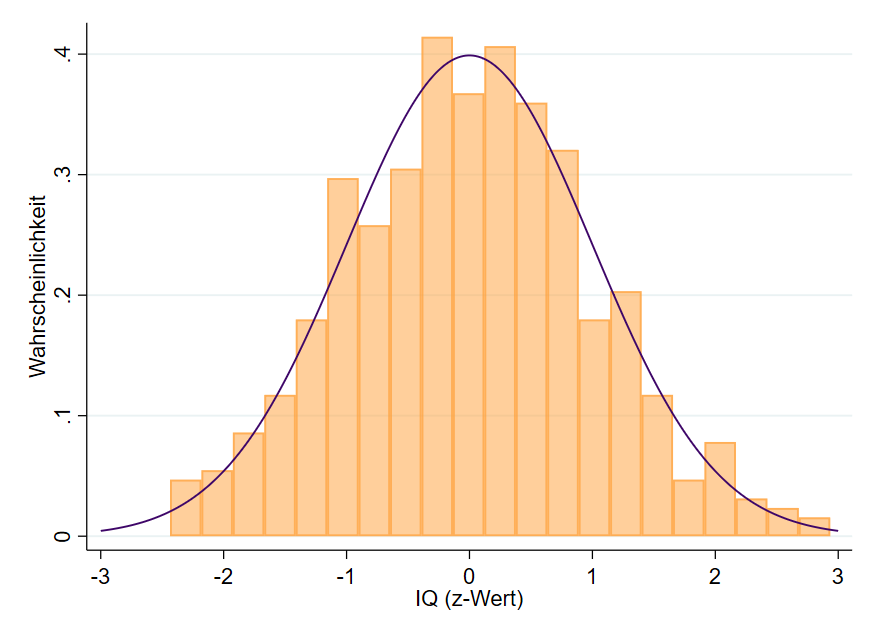
Die Standardnormalverteilung hat immer die Eigenschaften $\overline{x}=0$ und $s=1$. Auch unsere z-transformierte IQ-Variable hat nun diese Eigenschaften. Die Grundvoraussetzung, um mit dieser Verteilung arbeiten zu dürfen (!) ist, dass die Daten, die verwendet werden – also hier der IQ – auch normalverteilt sind, d. h. dass die Balken der Kurve »folgen«. Idealerweise sollten alle Balken unterhalb der lila Normalverteilungskurve liegen und zur Kurve selbst keine Lücken aufweisen. Da der IQ naturgemäß normalverteilt ist, werden wir dieses Beispiel fortführen dürfen. Am Ende des Themas wollen wir uns allerdings auch noch die Probleme bei einer nicht normalverteilten Variable ansehen.

Zwischenfazit

Da es sich hier um komplexere Zusammenhänge und Erklärungen handelt, wollen wir an dieser Stelle bereits eine Zusammenfassung machen.

1. Wir haben die Variable IQ – welche naturgemäß normalverteilt ist – aus unseren Daten z-transformiert und so eine neue Verteilung berechnet, die einen Mittelwert von $\overline{x}=0$ und eine Standardabweichung von $s=1$ aufweist.
2. Grafisch haben wir die Standardnormalverteilung (ebenfalls: $\overline{x}=0$ und $s=1$) in die Grafik hinzugefügt. Dargestellt ist die Kurve so, wie die Balken verlaufen müssten, wenn die Variable IQ normalverteilt wäre.
3. Die x-Achse sind jetzt z-Werte und keine original IQ-Werte mehr.

Wenn wir uns allein die Normalverteilungskurve ansehen, dann erweckt diese den Anschein, irgendwie aus dem Nichts entstanden zu sein. Aber auch hinter dieser Kurve liegt eine Häufigkeitsverteilung, nämlich exakt jene, die Gauß entdeckt hat. Wenn man die Balken an der x-Achse (z-Werte) extrem dünn darstellt, also die Bereiche sehr klein zusammenfasst und dann an das Ende der Balken eine Linie zieht, welche mathematisch geglättet wird (engl: smoothed), dann sieht eine Normalverteilungskurve inklusive Balken so wie in Abbildung 6 aus.

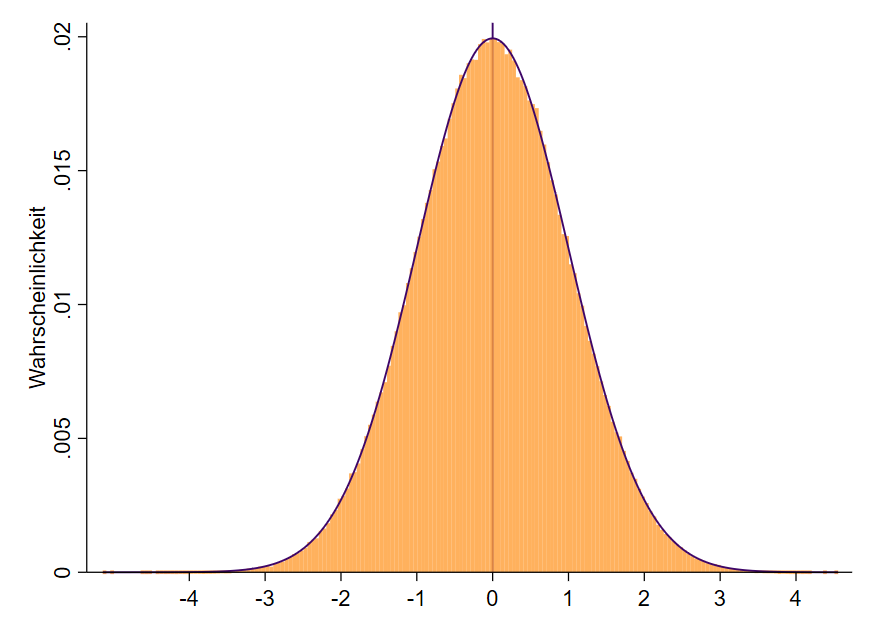
Hinter jedem winzigen Punkt der Kurve steht ein kleiner Balken, der eine Häufigkeit besitzt und damit in eine Wahrscheinlichkeit umgerechnet werden kann. In einer statistisch idealen Welt sollten also alle Daten so aussehen, damit wir klassische Statistik damit berechnen können. Wir wissen jedoch, dass dies nun mal nicht der Fall ist.

Eigenschaften der Standardnormalverteilung

Vielleicht erschließt sich dem Leser bereits jetzt, warum wir z-transformieren. Unsere IQ-Daten sind ohne eine Transformation mit der Standardnormalverteilung nicht vergleichbar, da Mittelwert und Standardabweichung nicht 0 und 1 sind. Aus diesem Grund muss eine Variable zunächst z-transformiert werden, um mit den Eigenschaften der Standardnormalverteilung verglichen werden zu können.

Die Standardnormalverteilung, welche im Folgenden aufgrund der Wortlänge nur noch als Normalverteilung bezeichnet wird, hat einige herausragende Eigenschaften, die wir mithilfe der sogenannten z-Tabelle (Tabelle 1 unten) herausfinden können. Diese Tabelle findet sich am Ende jedes Fachbuchs über die Grundlagen der Statistik und sieht (fast immer) so aus, wobei hier zunächst nur ein Ausschnitt dargestellt ist.

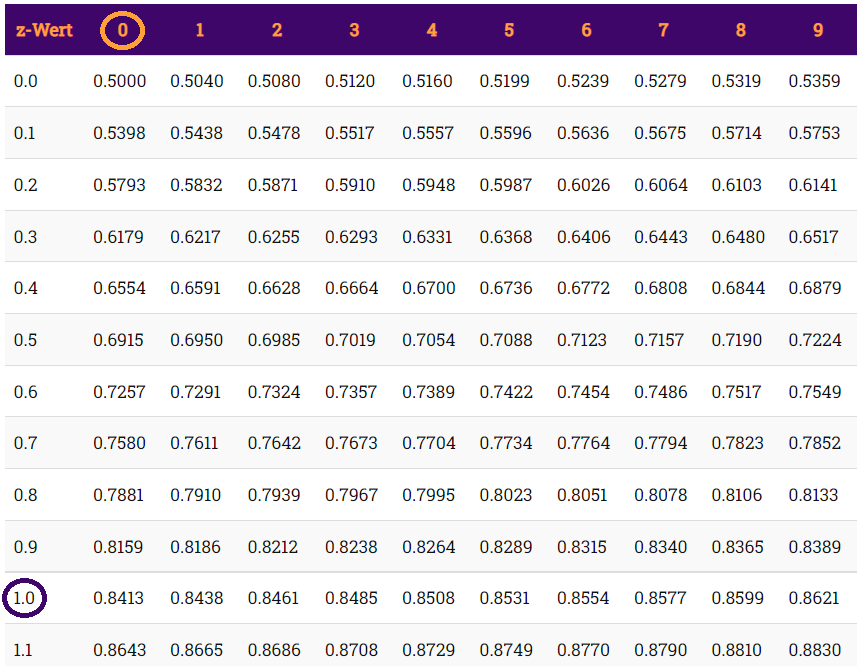
Normalerweise fängt die Tabelle bei 0 an und geht nach oben im positiven Bereich bis zu einem z-Wert von 3.0 oder 4.0, je nach Fachbuch. Einige Fachbücher stellen auch die negativen Werte dar, sodass die Tabelle von -4 oder -3 beginnend bis in den positiven Bereich geht. Die negativen z-Werte sind allerdings nicht notwendig, da die Normalverteilung symmetrisch ist: Alle Eigenschaften über dem Mittelwert von 0 treffen auch für die z-Werte unter dem Mittelwert zu.

Anhand dieser Tabelle können wir bestimmen, wie groß die Fläche – und damit also die Wahrscheinlichkeit – für einen bestimmten Balken ist oder einen Bereich von Balken. Wir interessieren uns als Erstes für die Wahrscheinlichkeit zwischen dem Mittelwert $\overline{x}=0$ und der Standardabweichung $s=1$, konkret $s=+1$”. Die Tabelle der z-Werte zeigt immer die Gesamtfläche / Wahrscheinlichkeit bis zu einem bestimmten Wert an. In unserem Fall suchen wir daher die Fläche bis zur Standardabweichung $s=+1$, also von ganz links (minus unendlich) bis $s=+1$ (Abbildung 7).

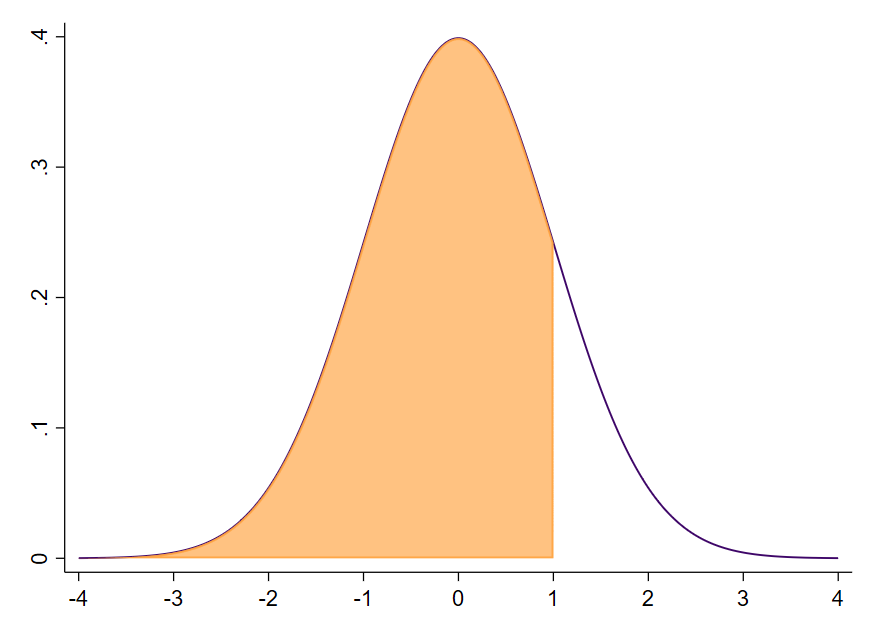
Den Wert der Fläche lesen wir in Tabelle 1 in der Zeile mit 1.0 ab (lila Kreis) sowie der Spalte mit der 0 (orangefarbener Kreis). Die Spalte gibt immer die 2. Nachkommastelle des z-Werts an. Ein Wert von 1.00 setzt sich als aus dem 1.0 der Zeile und der 0 der Spalte zusammen. Wir werden dies gleich noch üben. Die Größe der Fläche beträgt 0.8413, oder anders ausgedrückt: Die Wahrscheinlichkeit, dass ein Wert von (minus unendlich) bis zu +1 vorliegt, beträgt 0.8413 bzw. 84.13$. Dies entspricht der gesamten Fläche in Abbildung 7.

Uns interessiert allerdings die Wahrscheinlichkeit vom Mittelwert 0 bis $s=+1$, der dunkel orangen Fläche (Abbildung 8).

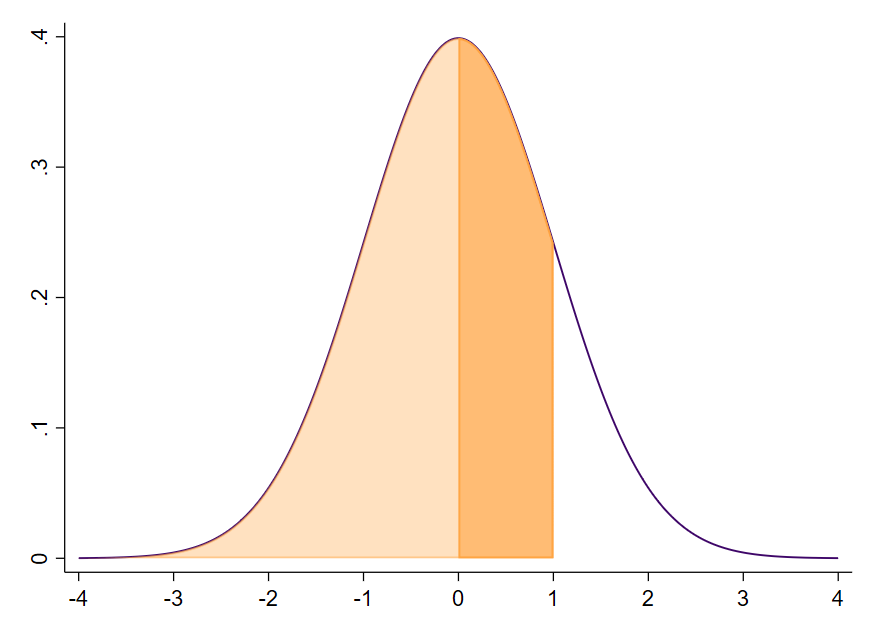
Bei einer symmetrischen Verteilung ist die Fläche bis zum Mittelwert 0.500 (helles orange in Abbildung 8), da die Gesamtfläche 1 ist. In der z-Wert Tabelle 1 lesen wir den Flächenwert für $z=0.00$ mit 0.500 ab. Der Mittelwert halbiert die Fläche unter der Kurve. Wir kennen damit alle Werte, um die Fläche / Wahrscheinlichkeit zwischen Mittelwert 0 und $s=+1$ zu berechnen. Wir ziehen die große Fläche (Abbildung 7) von der Fläche bis zum Mittelwert (Abbildung 8, helles orange) ab und erhalten die Fläche zwischen Mittelwert und Standardabweichung in Abbildung 8 (dunkles orange).

$$0.8413-0.500=0.3413$$

Die Fläche zwischen dem Mittelwert $\overline{x}=0$ und der Standardabweichung $s=+1$ hat einen Anteil von 34.13 %. Die Wahrscheinlichkeit, dass sich innerhalb dieses Bereichs ein Wert befindet, liegt bei 34.31 % oder $p=0.3413$.

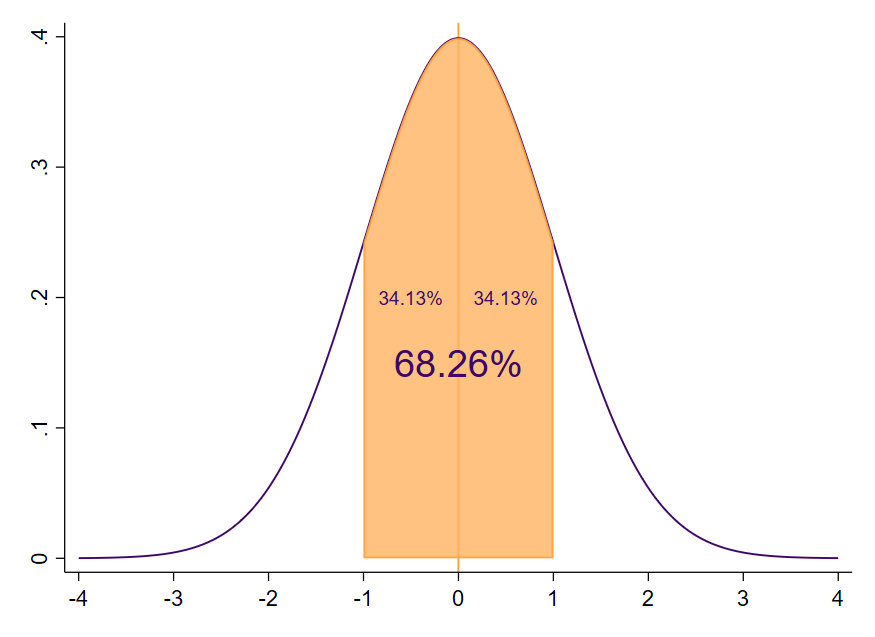
Da die Kurve symmetrisch ist, gilt die Fläche auch für die Standardabweichung $s=-1$, sodass wir die Gesamtfläche zwischen der Standardabweichung von -1 bis +1 berechnen können: $2*0.3413=0.6826$. Im Bereich einer Standardabweichung um den Mittelwert ($\overline{x}\pm1s$) liegt eine Fläche von 68.26 % (Abbildung 9).

Beispiel zur Flächenberechnung

Praktisch können wir so jede Flächen ausrechnen. Ein Beispiel: Uns interessiert die Fläche zwischen dem z-Wert -0.35 und +1.07 ($-0.35\leq\text{z}\leq1.07$), wie in Abbildung 10 dargestellt.

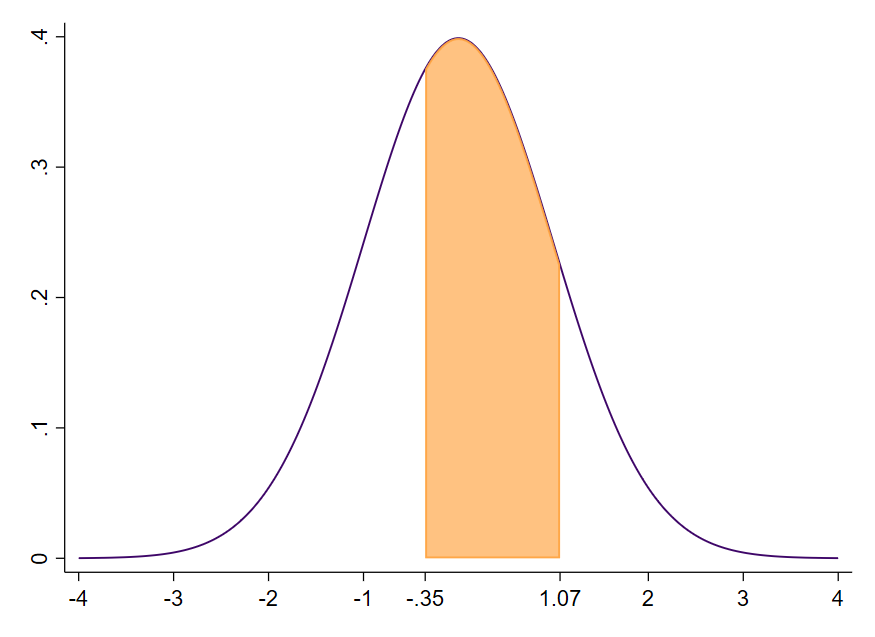
Der negative z-Wert $z=-0.35$ existiert in der z-Wert Tabelle in diesem Thema nicht, da die Tabelle bei 0 beginnt. Allerdings gibt es $z=0.35$. Zur Bestimmung der Fläche bis zu diesem Wert gehen wir in die Zeile mit 0.3 und dann in die Spalte mit der 5, was $z=0.35$ ergibt und einen Wert für die Fläche von 0.6368. Dies entspricht erneut der Gesamtfläche von minus unendlich bis $z=+0.35$.

Da dieser Wert über dem Mittelwert und der Fläche von 0.500 liegt, können wir erneut die Differenz bilden, um so die Fläche zwischen $z=0.00$ und $z=0.35$ zu bestimmen: $0.6368-0.500=0.1368$. Aufgrund der Symmetrie gilt die Fläche auch unterhalb des Mittelwerts, also zwischen Mittelwert und $z=-0.35$.

Fehlt noch die Fläche beim z-Wert von +1.07, genauer vom Mittelwert bis $z=1.07$. Hier lesen wir in der z-Wert Tabelle bei $z=1.07$ den Wert 0.8577 ab. Vom Mittelwert aus ist die Fläche somit $0.8577-0.500=0.3577$. Die Summe der soeben berechneten Teile ergibt die Fläche zwischen $z=-0.35$ und $z=+1.07$, also $0.1368+0.3577=0.4945$.

Was sagt uns diese Fläche?

1. Die Wahrscheinlichkeit, dass ein z-Wert von $-0.35\leq\text{z}\leq1.07$ vorliegt, beträgt $0.4945*100=49.45 \%$. Ist also recht wahrscheinlich.
2. Die Wahrscheinlichkeit, dass ein anderer z-Wert vorliegt, beträgt $1-0.4945=0.5055$, also 50.55 %.

Signifikanz und Normalverteilung

In der Statistik sprechen wir meist von einem Signifikanzniveau von 5 % ($p=.05$ oder $\alpha=5\%$). Die Logik dahinter leitet sich direkt aus der Standardnormalverteilung ab. Die Signifikanz von 5 % sind bei der Normalverteilung die unwahrscheinlichsten Daten. Diese befinden sich – da sie am wenigsten vorkommen – jeweils am Rand der Kurve, also im unteren (negativen) und oberen (positiven) Bereich.

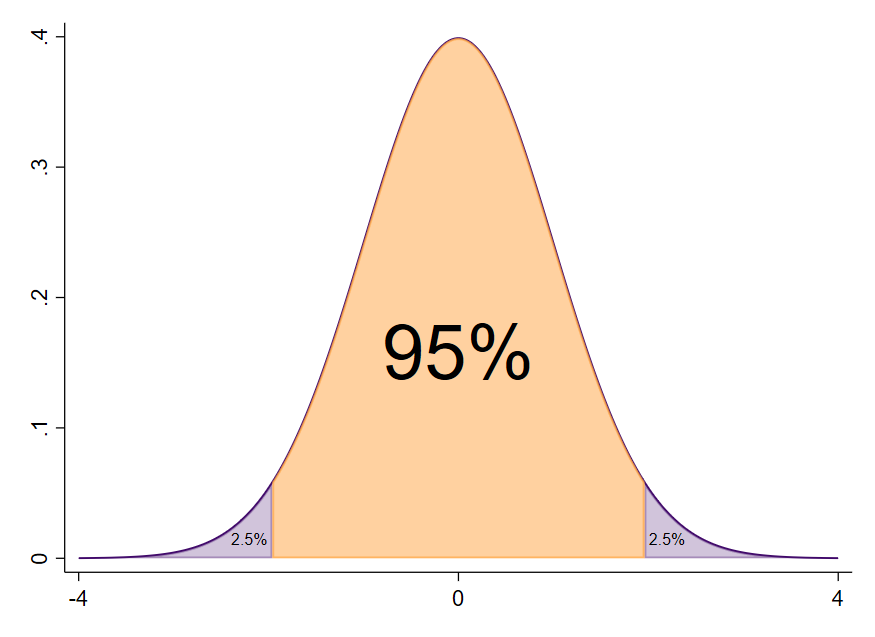
Dieser Bereich ist in Abbildung 11 lila dargestellt. Die unwahrscheinlichsten Werte einer Normalverteilung liegen jeweils zu 2.5% links und rechts gesehen unter der Kurve. Im restlichen Bereich liegen 95 % aller Werte (orange). Somit bleibt für uns herauszufinden, wo die Fläche von 2.5 % beginnt bzw. aufhört. Da die Verteilung symmetrisch ist, wäre es sicher am einfachsten zu schauen, wann die 2.5 % im oberen Bereich der Kurve (positiver Bereich) beginnen.

Dafür setzen wir ein wenig Logik ein: Wenn die lila Fläche ganz rechts 2.5 % ausmacht, dann ist die restliche Fläche bis zu dieser rechten blauen Fläche wie groß? Die Gesamtfläche beträgt 100 % und davon ziehen wir einfach 2.5 % ab und erhalten 97.5 %. Da die Tabelle der z-Werte für die Standardnormalverteilung uns immer die Fläche bis zu einem bestimmten Wert ausgibt, müssen wir jetzt in der Tabelle die Fläche von 97.5 % (0.975) finden und schauen, welcher z-Wert dazu gehört.

Öffnen wir hier dazu die Tabelle der z-Werte, da unsere Tabelle hier im Thema nur verkürzt dargestellt ist. Jetzt suchen wir die Fläche von 97.5%, also 0.975…
…und finden diesen Wert in der Tabelle relativ weit unten. Links lesen wir an der Zeile 1.9 ab und in der Spalte oben 6. Der z-Wert zu einer Fläche von 0.975 ist also $z=1.96$ im positiven Bereich bzw. $z=-1.96$ im negativen Bereich. Zwischen diesen beiden z-Werten befinden sich 95 % der Daten.

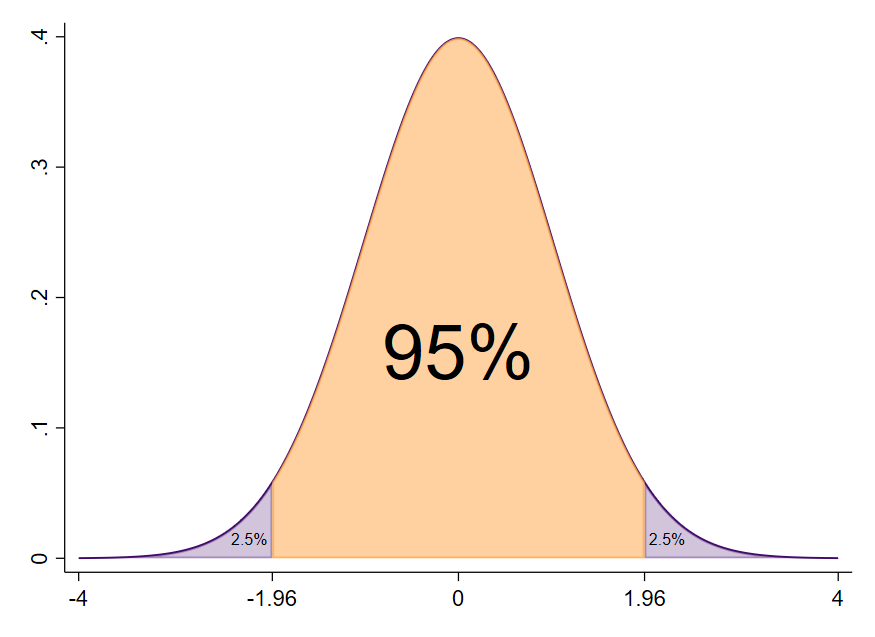
Die spannende Frage, die sich viele jetzt stellen, ist: Was können wir damit anfangen?

Anwendung: Vorteil der z-Transformation

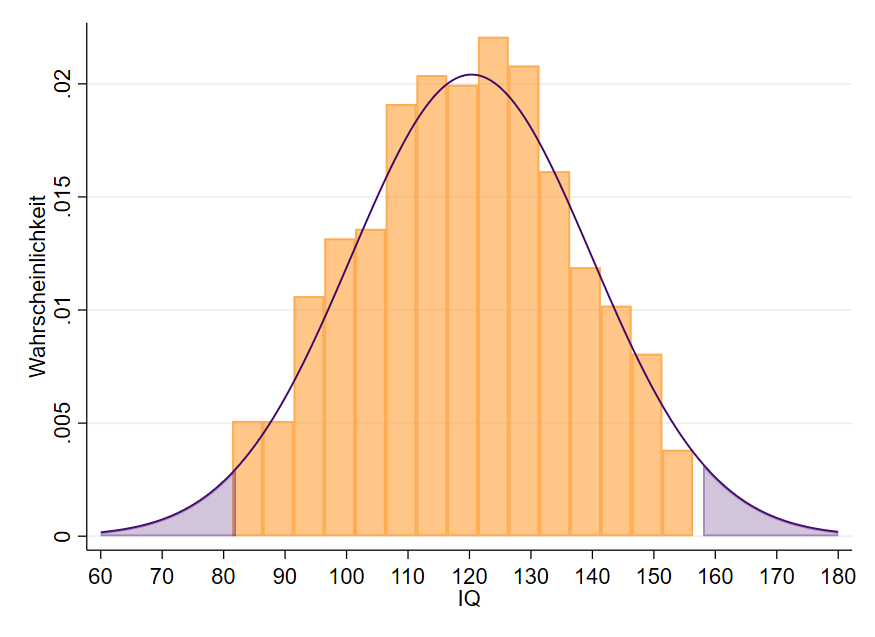
Kommen wir auf unsere IQ-Daten zurück (Abbildung 13). Rein optisch ist der IQ unserer Daten normalverteilt, was die Grundvoraussetzung ist, überhaupt mit der z-Wert Tabelle zu hantieren. Der Mittelwert in den Daten beträgt $\overline{x}=120.33$ und die Standardabweichung $s=19.548$. Wir interessieren uns für die 5 % der unwahrscheinlichen IQs in den Daten (lila Fläche in Abbildung 13) und wollen wissen, welche IQs dies sind.

Die Formel der z-Standardisierung lautet:

$$z=\frac{x-\overline{x}}{s}$$

Da wir wissen, dass ein z-Wert von $1.96$ jeweils die 2.5 % der Verteilung am Rande ausmacht, müssen wir also den IQ ($x$) finden, bei dem dieser z-Wert vorliegt. Dazu stellen wir die Formel um:

$$x=z*s+\overline{x}$$

Eingesetzt erhalten wir: $x=1.96*19.548+120.33=158.64$. Ein IQ von 158.64 entspricht einem z-Wert von 1.96 und damit liegen 2.5 % der Fälle über einem IQ $\geq158.64$.

Für den unteren Bereich der Kurve berechnen wir: $x=-1.96*19.548+120.33=82.02$. Der IQ von 82.02 entspricht dem z-Wert -1.96, so dass 2.5 % der Probanden einen IQ $\leq82.02$ in den Daten besitzen.

Die 5 % der unwahrscheinlichsten Fälle in unseren Daten finden wir bei einem IQ bis zu 82 und ab einem IQ von 159 (gerundet) vor. Dazwischen liegen 95 % unserer IQ-Daten.

Der Vorteil der z-Transformation zeigt sich hier noch einmal deutlich: Ein z-Wert von $1.96$ stellt immer die 2.5 % Grenze dar und verändert sich nicht. Somit lässt sich für jede Verteilung, welche normalverteilt ist, schnell diese und auch jede andere Fläche unter der Kurve berechnen. Wir legen damit eine der wichtigsten Grundlagen für die Inferenzstatistik, also die Statistik, in der wir den p-Wert berechnen und gegen den 5 % Grenzwert prüfen. Denn was wollen wir gern immer: Richtig, ein signifikantes Ergebnis! Über den Sinn und Unsinn dieser Behauptung sprechen wir allerdings in einem anderen Thema.

Schiefe Daten

Schauen wir uns am Ende dieser langen Ausführungen schiefe Daten an. Liegt eine Verteilung von schiefen Daten (orange in Abbildung 14) vor, die nicht der Normalverteilungskurve folgen, funktioniert die Logik der z-Werte nicht mehr. Die Kurve in Abbildung 14 selbst berechnet sich aus dem Mittelwert und der Standardabweichung unserer schiefen Daten und projiziert also die Kurve, wie die Daten aussehen müssten, wenn die Daten normalverteilt wären.

Wie wir in der Abbildung sehen können, existieren ab einem bestimmten Wert (rechts) keine Daten mehr, die Normalverteilungskurve »verlangt« aber praktisch danach. Die oberen 2.5 % existieren aus Sicht der Normalverteilungskurve also nicht, eine z-Transformation macht hier keinen Sinn. Außerdem existieren mit Blick auf die linke Seite der Verteilung deutlich mehr Werte, als dass es die Normalverteilung annehmen würde. Die Balken durchbrechen die Kurve sowohl an dieser Stelle, als auch weiter rechts deutlich.

Da die z-Transformation und deren Interpretation nur mit normalverteilten Daten funktioniert, wäre eine Interpretation von Flächen und z-Werten für diese vorliegenden Daten unzulässig. Statistische Signifikanz und Normalverteilung hängen grundlegend zusammen. Nicht normalverteilte Daten sind in der Statistik häufiger ein Problem, welches leider nicht immer korrekt betrachtet wird, da immer noch viele unterschiedliche Mythen und Legenden teils auch gelehrt werden, die einfach nicht stimmen.

Verwandte Themen

z-Transformation
z-Wert Tabelle der Standardnormalverteilung
Statistische Signifikanz